本文旨在用简单易懂的语言解释大语言模型的基本原理，不会详细描述和解释其中的复杂数学和算法细节，希望各位小猫能有所收获 🐱
AI 的科技树
我们先来通过一条简单的链路，定位大模型在 AI 领域的位置： 人工智能 > 机器学习 > 深度学习 > 大语言模型
机器学习最开始就用大量数据做线性回归从而对未知数据进行推测。
举个最简单的例子，二维的数据。直接就可以使用数学课就学过的线性回归求方程获取数据的趋势。
接着，人类不满足于简单的线性回归，想要让计算机自动学习更复杂的数据特征，于是就有了深度学习。
深度学习
深度学习之所以深度是因为，它基于多层神经网络自动学习数据特征。多层神经网络就像人脑的神经元互相连接。每根连接的强度就是权重，网络会反复调整这些强度，让结果越来越接近正确答案。
代表性模型有：卷积神经网络（CNN）、循环神经网络（RNN）、Transformer、GAN 等。
大语言模型
Transformer 无情压榨 GPU 产生的奇迹，起初应该没人觉得这效果能这么好。
与深度学习一样，Transformer 也是使用多层神经网络处理矩阵，只不过矩阵异常的大，不到硬件发展到一定水平根本无法实现。
关于大语言模型我们停一下，先比较基础的机器学习原理！
训练的方式
还是从最简单的二维数据开始。
当我们有一堆房产离市中心距离及其价格的数据时，我们可以在一个二维坐标轴表示这些数据，例如 x 轴是距离，y 轴是价格。
在数据都画上坐标轴之后，作为一个人类可能一眼就能粗略看出整个曲线的趋势，从而“拟合”出一条距离价格的关系。
它很可能是一个类似这样的函数：price = distance * w + b。
对于计算机，要求出 w 和 b 的最优解，就要让真实价格和通过 w b 计算出来的价格的差值最少。
最常用的方式是均方误差（Mean Squared Error, MSE）：
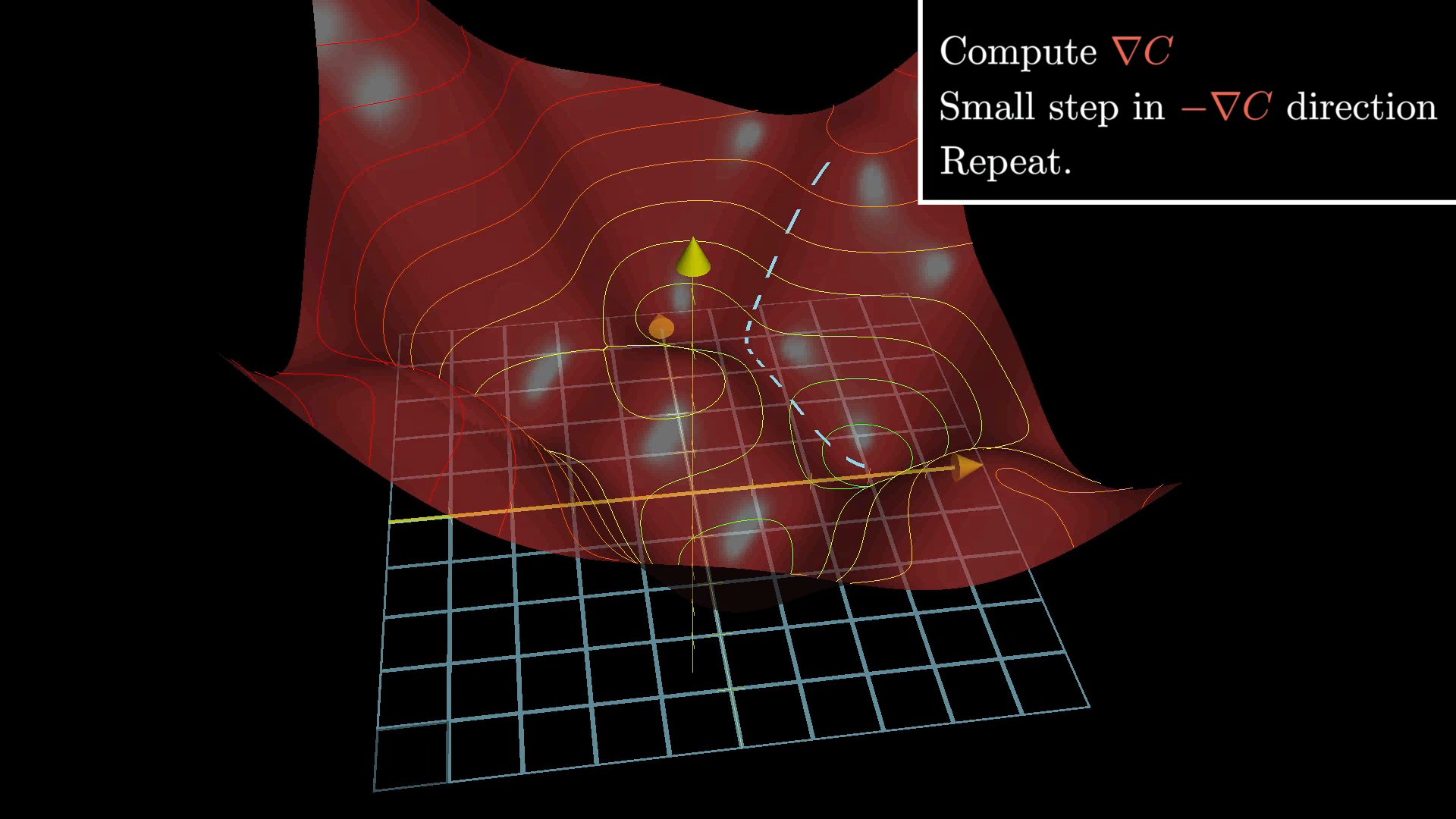
我们要求的就是这个函数的最小值，在人工智能领域常用的就是梯度下降，也就是求 w 和 b 的偏导数，乘上学习率 α，让它自己慢慢收敛。
过拟合
在拟合出一条接近“规律”的线条后，其实就差不多了。
如果你硬加更多的节点，会造成过拟合，也就所有的训练数据的损失值都很完美，但是一让它生成训练数据以外的东西，它就猜不准了。
就上面房价的例子，假如本来趋势基本就是一个斜线，但是你最后硬是求得一条曲线方程，把所有的点都穿过了，损失值为 0，但是这样计算用户给你的值，反而是算不准的。
这也就是所谓的失去泛化能力。
神经网络
上面只用二维数据，就只有一个 price = distance * w + b，但是如果想要做成神经网络，参数就会很多，并且与权重相乘的值的含义，人类并不能轻易理解，例如：
又因为如果只用权重，无论经过多少层都无法拟合曲线，所以最后要添加一个非线性的激活函数计算结果：
这只是一个层对某一个神经元的计算，下面是一个比较形象的图（请忽略数字）
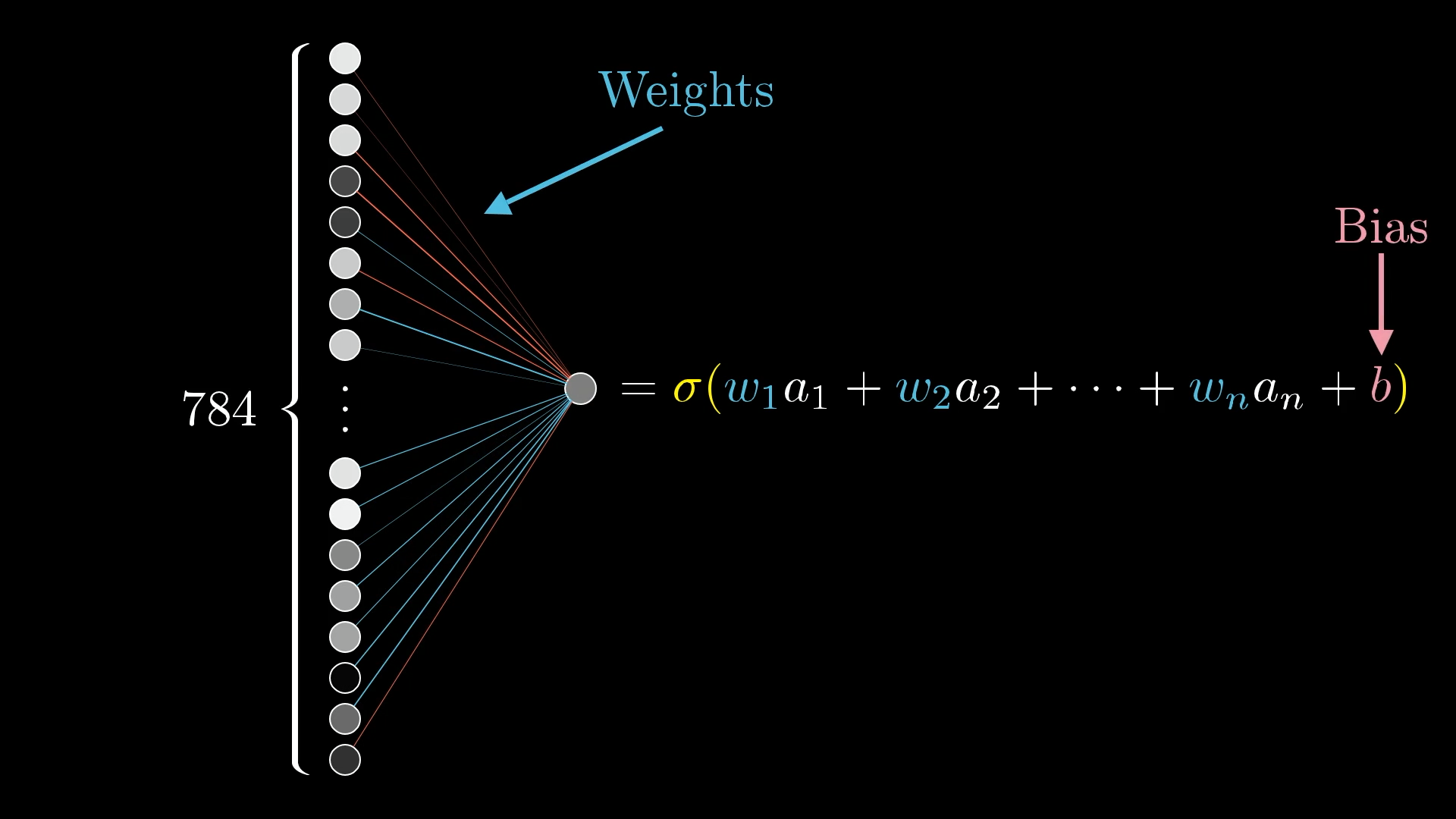
所以当一个神经网络有多层，每层多个神经元的话计算量还是挺可怕的。
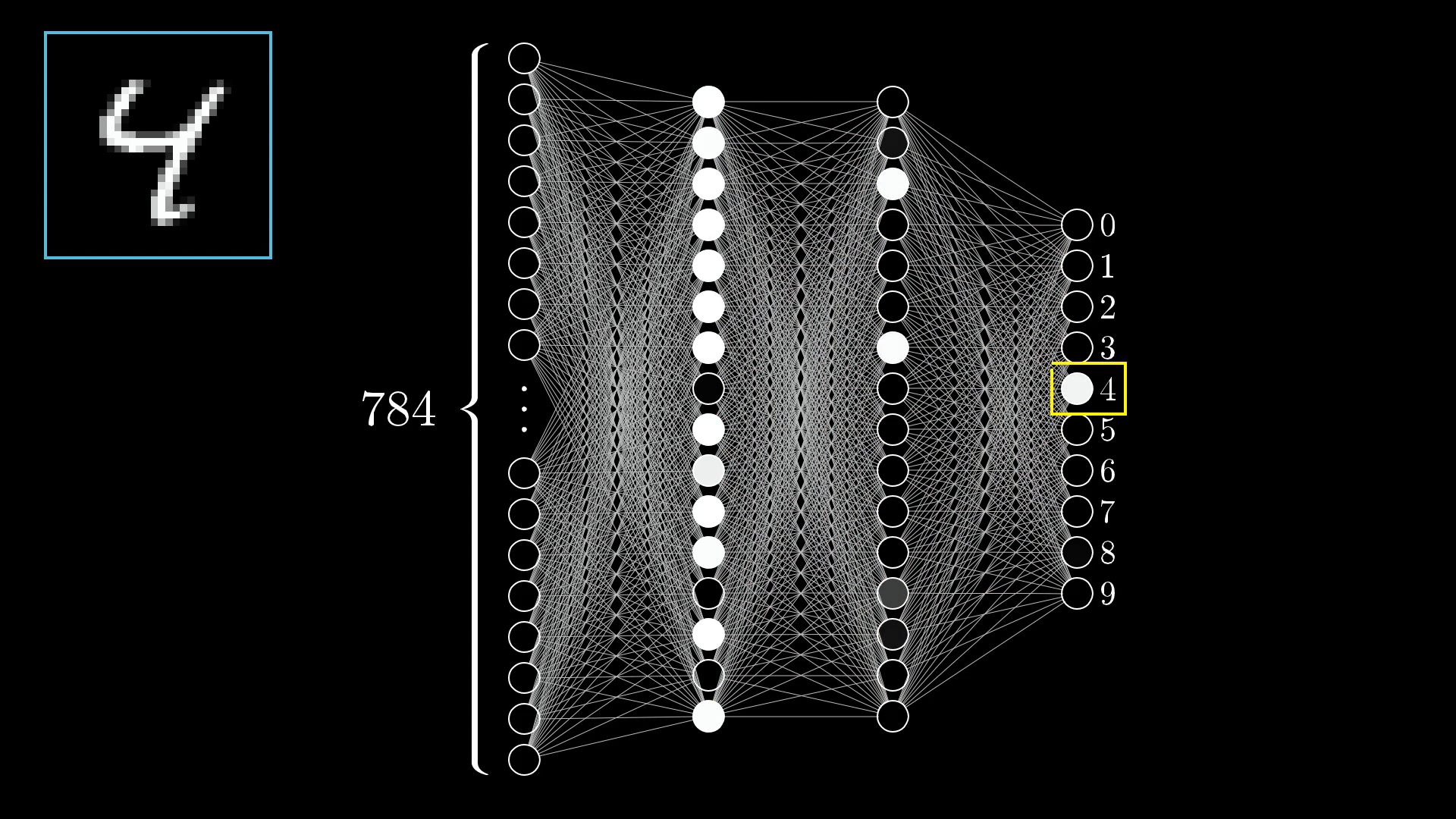
比如判断一张图片有没有猫，你没法用一条简单的线来划分”有猫”和”没猫”的区域。
多层网络的魔力在于：
- 逐层特征提取：第一层可能只学到边缘和颜色，第二层学到边缘组成的形状，第三层学到眼睛、耳朵，第四层才认识完整的猫脸
- 非线性组合：通过激活函数，每一层都能创造新的特征组合，让网络可以表示任意复杂的函数
- 层次化抽象：就像人类认识世界一样，先学简单概念，再组合成复杂概念
这就等于在计算的时候把数据的内涵升维到隐藏层，经过隐藏层额外的处理可以得到更精确的结果。当然这个时候你输入的值也要有足够的信息量它才能学到东西。
但问题又来了既然多层这么强大，那是不是层数越多越好？也不是的。神经网络有两个维度可以调整：
深度（Deep）：层数多，每层神经元少
- 参数少，计算效率高
- 适合层次化特征学习
- 容易出现梯度消失（层数太多，误差传不到前面）
- 训练困难
宽度（Wide）：层数少，每层神经元多
- 训练相对简单
- 能并行处理更多信息
- 参数量大，容易过拟合
- 缺乏层次化抽象能力
实际训练时深度和宽度的平衡需要把握好。
反向传播
上面我们知道用梯度下降的方式调节 w 和 b，对于神经网络也是一样的数学原理，需要通过链式法则（Chain Rule）一层一层反向调整所有权重。
这里就不详细解释怎么层层反推了，就结果而言，我们给出了正确的输入和输出，最开始，这个网络只是瞎猜权重，到最后计算出来，经过损失函数梯度下降调整各种权重，到最后，竟然就可以像魔法一样推导出准确率比较高的答案，喵，喵，喵呀！
P.S. 如果你真的找虐很想了解更多反向传播的计算过程，可以看 3blue1brown 🐱