注意事项:
- 本文仅涉及 WebGL1.0
- 本文仅涉及 fragment shader
- 本文重点参考对象:The Book of Shaders
- 一些图片来源于 open.gl
- 下面所有例子都可以贴到这个 Playground 直接运行
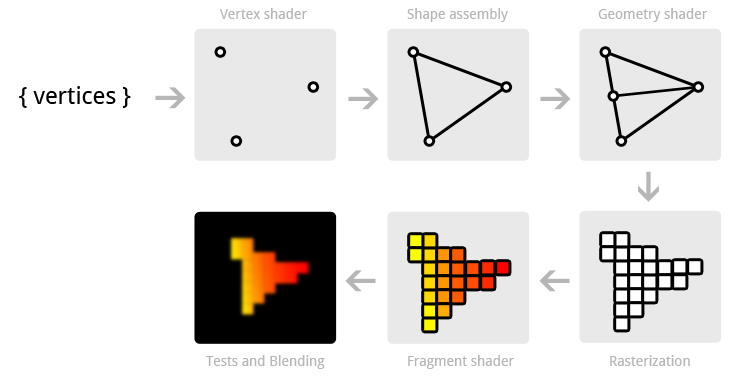
本质
从上面流水线的图也能看出来,fragment shader 的本质就是对每个(像素)点作处理。大家都知道 GPU 擅长并行的简单计算,目的就是要做好这件事。相反,CPU 擅长复杂计算,但处理器却很少。
The Book of Shaders 给出一个形象的比喻:
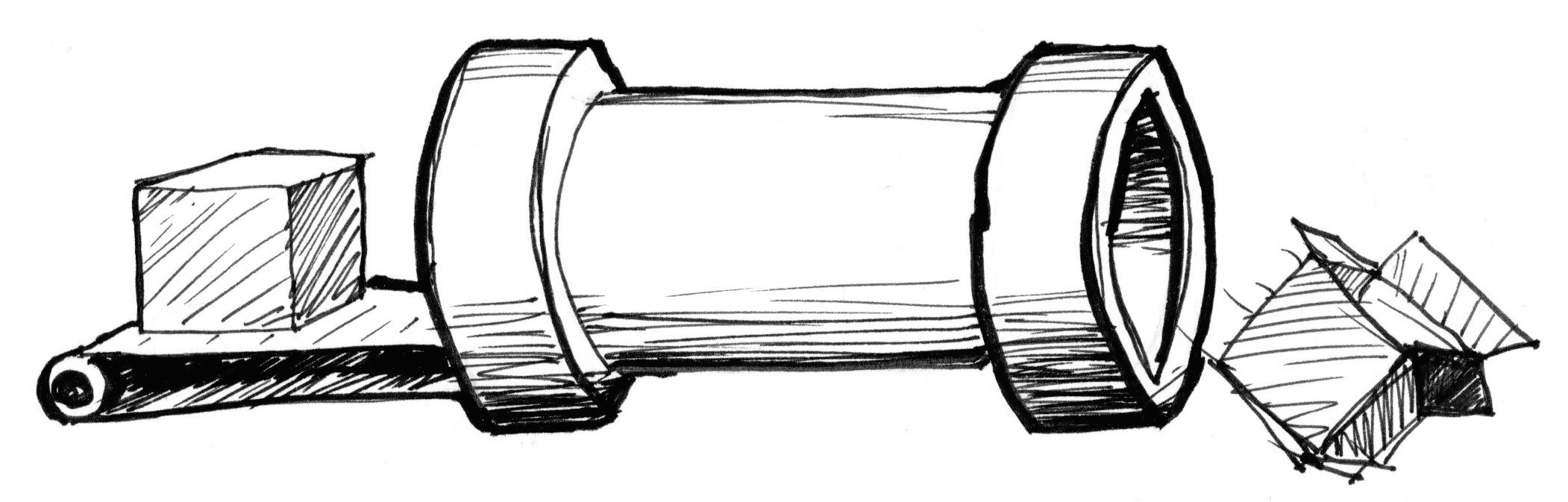
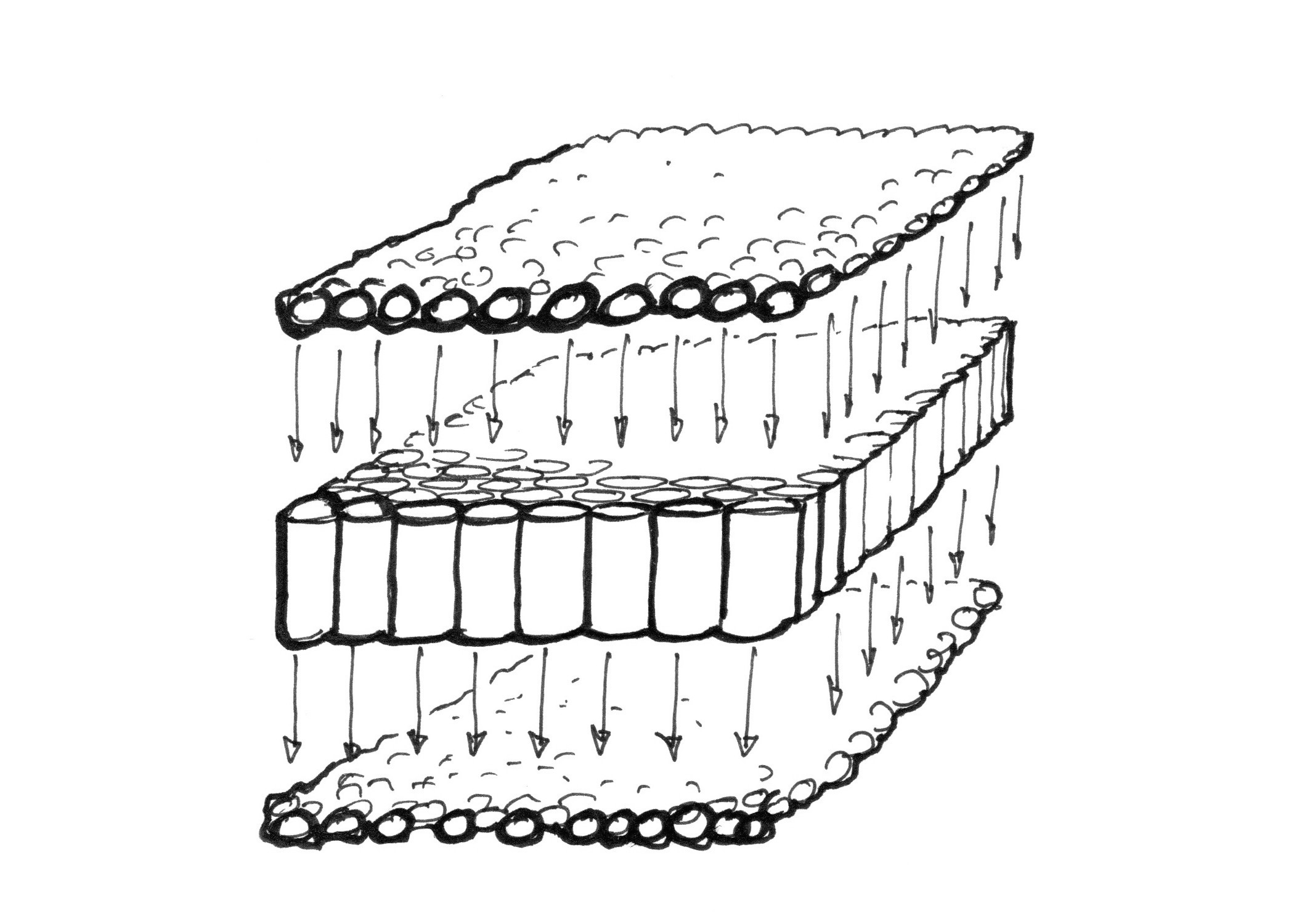
uniform
uniform 之所以叫 uniform 是因为它是统一的。由 CPU 传到 GPU,在处理每一个像素时,这个值都是统一的。相对的是 varying,这些值由 vertex shader 计算后传到 fragment shader,针对每个三角形,收到的值是不一致的。
输入输出
uniform vec2 u_resolution;
void main() { // `gl_FragCoord.xy/u_resolution` 将 xy 值映射为 0 到 1 vec2 st = gl_FragCoord.xy/u_resolution; gl_FragColor = vec4(st.x,st.y,0.0,1.0);}gl_FragCoord 是内置输入,表示一个点的位置;gl_FragColor 是固定的输出值,表示这个点应该显示为何种颜色。
映射
关键输入是位置,关键输出是颜色,那么很明显,要使用 fragment shader 绘图的重点就是找到位置和颜色的关系,也可以说 GPU 要做的就是要计算每个点的颜色。再换一个说法就是你要发挥你的聪明才智,利用位置 x 和 y 的关系生成一个好看的图像。
所以为什么 0 到 1 的映射这么重要呢,因为 webgl 的 rgb 输出就是 0 到 1 的范围,这是构建位置和颜色关系最直接的方式。此外,像 smoothstep 和 fract 这样的重要内置函数都返回范围为 0 到 1 的值。
在上面的例子中,首先将 gl_FragCoord 映射为 0 到 1,然后分别把 x 和 y 值放到 r 和 g,(左下角是 0,0)所以出来的图像左下角黑色,左上角红色,右下角绿色。
P.S. WebGL2 的输出方式不一样
常用函数
为了画出各种花里胡哨的图形,我们必须了解这些常用的函数:
角度和三角函数相关
指数相关
常用数学方法
- abs() 绝对值
- sign(x) 把 x 映射为 0、1、-1
- floor() 向下取整
- ceil() 向下取整
- fract() 只取小数部分
- mod(x, y) 对 x 取模
- min(x, y) 返回两值中较小值
- max(x, y) 返回两值中较大值
- clamp(x, minVal, maxVal) 仅在最大最小值范围内变化,超出范围时输出边界值
- mix(x, y, a) 从 x 渐变到 y,a 是变换的“进度”
- step(edge, x) 一种突变,将 x 映射为 0 到 1,小于 edge 返回 0,否则返回 1
- smoothstep(edge0, edge1, x) 在 edge0 和 edge1 的区间内,将 x(使用 Hermite interpolation)丝滑地映射为 0 到 1,需要注意的是改变 edge0 和 edge1 顺序的话效果是不一样的
GEOMETRIC FUNCTIONS
- length() 一个向量的长度
- distance() 两个点的距离,其实跟 length 差不多是一个东西了,只是解读的角度有点不同
- dot() 向量点积
- cross() 向量叉积
- normalize() 返回单位向量
- facefoward() 返回与参考向量指向相同方向的向量
- reflect() 反射计算
- refract() 折射计算
可以开始画了吗!
可以!在了解上面一堆常用函数之后,你已经可以画出出神入化的图像了!例如下面这样的简短的代码就能营造一种熔岩灯的感觉(看效果戳这里):
// Author @patriciogv - 2015// http://patriciogonzalezvivo.com
#ifdef GL_ESprecision mediump float;#endif
uniform vec2 u_resolution;uniform vec2 u_mouse;uniform float u_time;
vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); }
float snoise(vec2 v) { const vec4 C = vec4(0.211324865405187, // (3.0-sqrt(3.0))/6.0 0.366025403784439, // 0.5*(sqrt(3.0)-1.0) -0.577350269189626, // -1.0 + 2.0 * C.x 0.024390243902439); // 1.0 / 41.0 vec2 i = floor(v + dot(v, C.yy) ); vec2 x0 = v - i + dot(i, C.xx); vec2 i1; i1 = (x0.x > x0.y) ? vec2(1.0, 0.0) : vec2(0.0, 1.0); vec4 x12 = x0.xyxy + C.xxzz; x12.xy -= i1; i = mod289(i); // Avoid truncation effects in permutation vec3 p = permute( permute( i.y + vec3(0.0, i1.y, 1.0 )) + i.x + vec3(0.0, i1.x, 1.0 ));
vec3 m = max(0.5 - vec3(dot(x0,x0), dot(x12.xy,x12.xy), dot(x12.zw,x12.zw)), 0.0); m = m*m ; m = m*m ; vec3 x = 2.0 * fract(p * C.www) - 1.0; vec3 h = abs(x) - 0.5; vec3 ox = floor(x + 0.5); vec3 a0 = x - ox; m *= 1.79284291400159 - 0.85373472095314 * ( a0*a0 + h*h ); vec3 g; g.x = a0.x * x0.x + h.x * x0.y; g.yz = a0.yz * x12.xz + h.yz * x12.yw; return 130.0 * dot(m, g);}
void main() { vec2 st = gl_FragCoord.xy/u_resolution.xy; st.x *= u_resolution.x/u_resolution.y; vec3 color = vec3(0.0); vec2 pos = vec2(st*3.);
float DF = 0.0;
// Add a random position float a = 0.0; vec2 vel = vec2(u_time*.1); DF += snoise(pos+vel)*.25+.25;
// Add a random position a = snoise(pos*vec2(cos(u_time*0.15),sin(u_time*0.1))*0.1)*3.1415; vel = vec2(cos(a),sin(a)); DF += snoise(pos+vel)*.25+.25;
color = vec3( smoothstep(.7,.75,fract(DF)) );
gl_FragColor = vec4(1.0-color,1.0);}开玩笑的,离独自构思出这种图像还有很大一段距离 😂
0 到 1 有几种走法
在实际使用中,必定不可能只存在线性关系,所以利用各种函数调整 xy 和 0 到 1 的映射,是学习编写 fragment 不能绕过的一步。
在 The Book of Shaders 中,作者使用 plot 函数将映射关系可视化,同时将 x 值的映射赋给 gl_FragColor,这样可以比较直观地看到不同曲线的实际效果:
// Author: Inigo Quiles// Title: Pcurve
#ifdef GL_ESprecision mediump float;#endif
uniform vec2 u_resolution;uniform vec2 u_mouse;uniform float u_time;
// Function from Iñigo Quiles// www.iquilezles.org/www/articles/functions/functions.htmfloat pcurve( float x, float a, float b ){ float k = pow(a+b,a+b) / (pow(a,a)*pow(b,b)); return k * pow( x, a ) * pow( 1.0-x, b );}
float plot(vec2 st, float pct){ return smoothstep( pct-0.02, pct, st.y) - smoothstep( pct, pct+0.02, st.y);}
void main() { vec2 st = gl_FragCoord.xy/u_resolution;
float y = pcurve(st.x,3.0,1.0);
vec3 color = vec3(y);
float pct = plot(st,y); color = (1.0-pct)*color+pct*vec3(0.0,1.0,0.0);
gl_FragColor = vec4(color,1.0);}渲染结果可以直接点这里
方与圆
float rect (vec2 st,float width){ // bottom-left vec2 bl = step(vec2(0.5-width/2.),st); float pct = bl.x * bl.y;
// top-right vec2 tr = step(vec2(0.5-width/2.),1.0-st); pct *= tr.x * tr.y; return pct;}
float circle(in vec2 _st, in float _radius){ vec2 dist = _st-vec2(0.5); return 1.-smoothstep(_radius-(_radius*0.01), _radius+(_radius*0.01), dot(dist,dist)*4.0);}
void main(){ vec2 st = gl_FragCoord.xy/u_resolution.xy; vec3 rectcolor = vec3(rect(st,.5)); vec3 circlecolor = vec3(1) - vec3(circle(st,.5));
gl_FragColor = vec4(circlecolor + rectcolor,1.0);}方圆是最容易理解的图形,上面的代码又几个需要注意的点:
- 方形的代码有一点长,不过其实注意一下以乘法制造交集就好了
- 例子中使用的点积画圆形,因为点积就是两个向量的投影关系,所以自己投到自己身上就是一种计算长度的方法
- 当然你也可以使用
length、distance甚至自己用两点间距离算法来画圆 - 画圆形(或者说曲线)也不是不可以用
step,只是使用smoothstep会有抗锯齿效果 - 程序员的好朋友抽象永远能帮你实现更高效简洁的代码,你可以轻易调个函数画出复杂的图形(即使暂时没看懂绘图的原理)
小星球
一些手机图片处理应用会有一个叫“小世界”的滤镜,其实就是把图片从笛卡尔坐标映射成极坐标。如果我们希望用 fragment shader 画出雪花、齿轮等图形,可以根据同样的道理把对应的“波形”映射到极坐标,代码如下:
void main(){ vec2 st = gl_FragCoord.xy/u_resolution.xy; vec3 color = vec3(0.0);
vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0; float a = atan(pos.y,pos.x);
float f = cos(a*3.); // 3 瓣 // f = abs(cos(a*3.)); // 6 瓣 // f = abs(cos(a*2.5))*.5+.3; // 5 瓣 // f = abs(cos(a*12.)*sin(a*3.))*.8+.1; // 雪花 // f = smoothstep(-.5,1., cos(a*10.))*0.2+0.5; // 齿轮
color = vec3( 1.-smoothstep(f,f+0.02,r) );
gl_FragColor = vec4(color, 1.0);}a通过反正切求出点与中心连线的角度,相当于原本的 X 轴,返回值为 -PI 到 PIr可以理解为原本的 Y 轴f则是 Y 轴的值,color 就是用smoothstep分割f,小于f显黑,大于f显白- 所以顺眼的写法其实是
float y = cos(x*3.); - 通过将不同函数映射到极坐标可以产生各种有意思的形状
Pattern
这里的 Pattern 不是设计模式,而是指重复的图案。之前讲的都是单个图案,那么怎么批量生成一大堆排列整齐的图案呢?
答案是fract()。
void main() { vec2 st = gl_FragCoord.xy/u_resolution; vec3 color = vec3(0.0);
st *= 3.0; // Scale up the space by 3 st = fract(st); // Wrap around 1.0
// Now we have 9 spaces that go from 0-1
color = vec3(st,0.0); // color = vec3(circle(st,0.5));
gl_FragColor = vec4(color,1.0);}人类的本质是复读机,而 fract() 可以算是 GLSL 的复读机了吧 😅,通过 fract() 可以让数值在 0 到 1 间的小数中不断循环。
- 首先将 xy 值映射为 0 到 1
- 再将其映射为 0 到 3
- 经过
fract()的处理,就会变成复读 3 次 0 到 1,效果就出来了
伪随机
对于生成图像,也不涉及金钱交易什么的,伪随机就够用了,至于真正的随机,用到硬件噪声等无法预测的输入,这里暂不讨论。
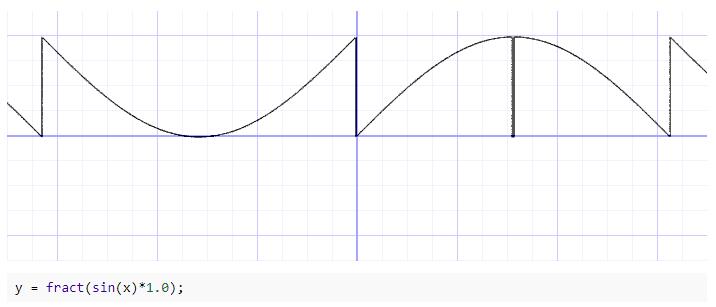
y = fract(sin(x)*1.0); 就是伪随机的基础(之一)。虽然从连续的图像上看,非常规律,但是要是以 x 为整数,取 y,作为一个正常人类未必能反应出来这就是一个普通的 sin,我们使用 JavaScript 输出一下整数作为参数输出的“随机值”:
function fract(num) { return Math.abs(num - Math.trunc(num));}function random(x) { return fract(Math.sin(x) * 1);}const nums = [];for (let i = 1; i < 20; i++) { nums.push(random(i));}// output=> [0.8414709848078965, 0.9092974268256817, 0.1411200080598672, 0.7568024953079282, 0.9589242746631385, 0.27941549819892586, 0.6569865987187891, 0.9893582466233818, 0.4121184852417566, 0.5440211108893698, 0.9999902065507035, 0.5365729180004349, 0.4201670368266409, 0.9906073556948704, 0.6502878401571168, 0.2879033166650653, 0.9613974918795568, 0.7509872467716762, 0.14987720966295234]在这个基础上,sin(x) 的乘数越大,结果看起来就越随机:
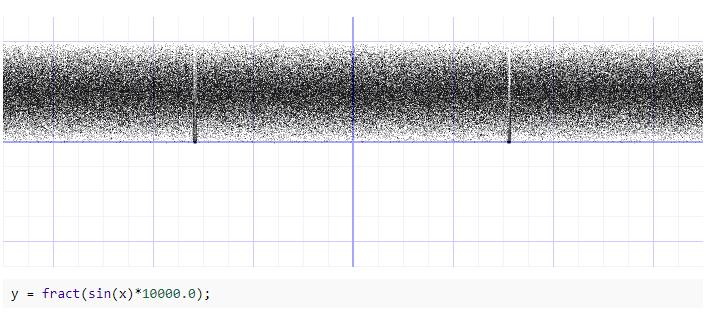
现在我们知道可以用 y = fract(sin(x)*10000.0); 把 x 映射为伪随机的 0 到 1,那么接下来就很简单了吧?把像素位置映射为随机数,然后把随机数设置为输出颜色,便能看到随机图像。
float random (vec2 st) { return fract(sin(dot(st.xy, vec2(12.9898,78.233)))* 10000.0);}
void main() { vec2 st = gl_FragCoord.xy/u_resolution.xy; // st = st * 15.; // st = floor(st); float rnd = random( st );
gl_FragColor = vec4(vec3(rnd),1.0);}上面的代码可以绘制出类似雪花屏的效果,需要注意的是 random 函数中的“x”是用 xy 值与一个向量求点积(投影长度)所得。如果想要马赛克也很简单,用之前的复读方法映射一下就完事啦(去掉两个注释可以看到效果)!
